Research

Bootstrap Embedding

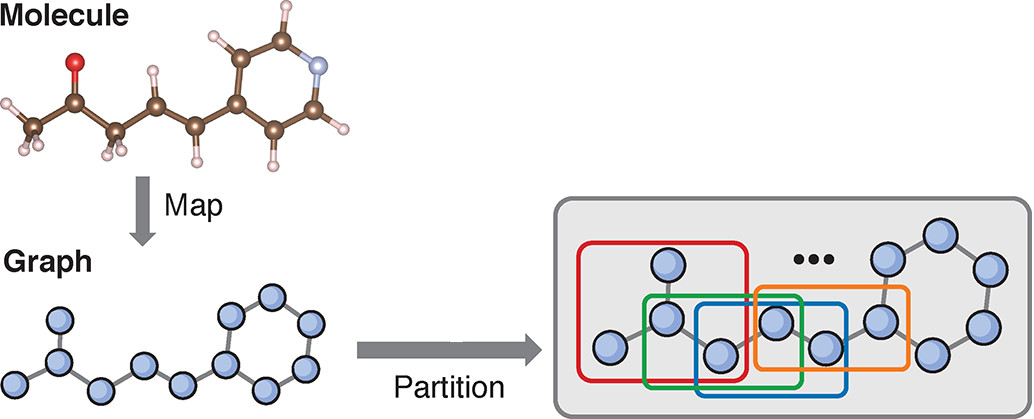
Embedding methods, broadly speaking, aim to reduce the cost of large calculations by treating parts of a chemical system with different levels of theory, relying on the intrinsically local nature of electron correlation in their approximations. By treating small fragments within the system with high-accuracy theories while describing the surrounding bath with less expensive methods, embedding techniques attempt to capture important chemical information for increasingly large systems.

In the Van Voorhis group, we have developed a Schmidt Decomposition-based fragment embedding method in which the system is partitioned into overlapping fragments, each centered around a single site or atom. We treat all fragments with a high-level methodology while imposing matching conditions between the center (best-described) and edge sites in overlapping fragments. In this way, the method “pulls itself up by its own bootstraps” to evenly treat the entire system with the high-level wavefunction methodology.

Bootstrap Embedding has seen success in our group for lattice models and simple molecular systems. We have extended the success of Bootstrap Embedding to molecules, where fragments can be naturally defined based on atomic connectivity, in a variety of applications. Current work in our group focuses on improving and applying Bootstrap Embedding in the context of real molecules in large basis sets; applying Bootstrap Embedding to periodic systems; work with alternative wavefunction solver methods; and application towards quantum computing.

QuEmb(Docs) is an open-source package for Bootstrap Embedding calculations actively developed in the group.

Quantum Dots

Our group investigates the geometry - electronic structure relationships of nanocrystals, especially colloidal quantum dots, in the ground and excited states. Implementation of nanocrystals in photovoltaic and photoemissive devices is hampered by mid-gap electronic states known as trap states, which are often associated with surface defects. Our group has investigated the nature and origin of these trap states in II-VI and III-V semiconductor nanocrystals, finding differing behavior in the two classes of materials, new types of trap states not previously described in these nanocrystals, and specific trends related to site coordination number, species, geometry, and electrostatic environment which influence trap presence and depth. We have further investigated how trap states are affected by surface reconstruction and how they are influenced by the presence of an inorganic shell.

Through collaboration with experimental groups at MIT and further afield, we have leveraged our expertise in nanocrystal electronic structure to study the geometry and ligand binding preferences of lead halide perovskite nanoplatelets and the X-ray photoelectron spectra of InGaP mesas. Moreover, we have developed a super-resolution technique known as the Broad Yet Narrow Description (BYND) for accurately simulating entire absorption spectra of large material systems at a fraction of the traditional cost. BYND does this by optimizing a highly approximate TD-DFT spectrum obtained with the Small Matrix Approximation (SMA) to fit a high accuracy but low resolution short time signal obtained from real-time TD-DFT. Along a similar vein, current work focuses on utilizing a kernel ridge regression to learn guess Hamiltonian - converged Hamiltonian mappings for specific systems to extend ab-intio molecular dynamics (AIMD) simulations for large systems to far longer timescales. Most DFT studies of nanocrystals ignore thermal and ensemble effects, which precludes direct comparison with experimental absorption and emission spectra. The conventional method to generate thermally averaged spectra is the Nuclear Ensemble Approach (NEA), which requires extensive sampling and is prohibitively expensive for QDs beyond the ultrasmall regime. To address this issue, our group proposes a less resource-intensive approach: the Harmonic Approximation (HA), which assumes the electronic potential energy surfaces of QDs to be harmonic, with excited states having the same curvature as the ground state. Absorption spectra for QDs computed with the equilibrium HA accurately capture thermal broadening and Urbach band tailing, at a fraction of the cost of the NEA method.

We are also interested in examining exciton-phonon coupling, using the Huang-Rhys (HR) factor metric. Our findings suggest that the degree and effectiveness of surface passivation has a sizeable effect on the magnitude of exciton-phonon coupling. Successful passivation strategies for nanocrystals should not only minimize the number of trap states, but also reduce the spatial overlap between excitons and phonons, thereby lowering the HR factors.

Quantum Computing

Computational chemistry is one of the areas where quantum computing may have the most significant impact. Within electronic structure theory, different eigensolver algorithms, such as quantum phase estimation (QPE) and variational quantum eigensolver (VQE), can provide alternative pathways for calculating single-point energies of chemical Hamiltonians. Near-term quantum devices, however, lack the number of qubits and gate depth necessary to apply these algorithms to chemical systems of interest.

Through our work with collaborators, we proposed a multiscale embedding approach that utilizes both quantum and classical computing resources. Starting from solvated protein complexes comprised of many atoms, we first choose a region of interest to treat on a quantum mechanical level. Then, within the quantum mechanical region, we use Bootstrap Embedding to partition the area into smaller chunks that produce smaller Hamiltonians amenable for near-term quantum devices. This results in a QM/QM/MM embedding that can efficiently exploit the capabilities of quantum computers to account for correlation effects. Other techniques in our papers allow fine-grained and systematic control over the required quantum resources and the target accuracy.